බලය (force) යනු කුමක් දැ යි ඔබ මීට පෙර පන්තිවල දී හදාරා ඇත. යමක් තල්ලු කිරීමේ දී අප කරන්නේ බල යෙදීමකි. යමක් ඇදීමේ දී කරන්නේ ද බල යෙදීමකි. එසැවීම, තෙරපීම ආදී මේ සියල්ල ම සිදු වනුයේ බල යෙදීම හේතුවෙනි. නිශ්චල වස්තුවක් චලනය කිරීමට අප කුමක් කළ යුතු ද? එය චලනය කිරීමට අවශ්ය දිශාවට බලයක් යෙදිය යුතු ය. එහෙත් බලයක් යෙදූ පමණින් ම එහි චලනය ඇරඹේ ද?

මේසයක් 4.1 රූපයේ පෙන්වා ඇති ආකාරයට තල්ලු කර බලන්න. චලනය ආරම්භ නොවේ නම් යොදන බලය වැඩි කර තල්ලු කරන්න. මෙසේ බලය වැඩි කරන විට එක් අවස්ථාවක දී එය චලනය වීම ආරම්භ වෙයි. මේසය තල්ලු කළ ආකාරයට ම ඔබ තනිවම බසයක් තල්ලු කළහොත් එය චලනය නොවේ. නමුත් 4.2 රූපයේ මෙන් තවත් පිරිසකගේ ආධාරය ඇතිව බසය තල්ලු කළහොත් එය චලනය වනු ඇත. එනම් යොදන බලය වැඩි කළ විට බසය චලනය වීම ඇරඹෙයි.
මෙම අවස්ථා දෙකෙහි දී ම සිදුවන්නේ වස්තුව මත යොදන බලය එම වස්තුවේ චලිතයට බාධා පමුණුවන යම් බලයක් අභිබවා ගිය විට එම වස්තුව චලනය වීම ආරම්භ වීමයි. එම වස්තුවේ චලිතයට බාධා පමුණුවන බලය ඝර්ෂණය නමින් හැඳින්වෙන ප්රතිරෝධී බලයකි. අප යොදන බලය කුඩා නම් එම බලය ප්රතිරෝධී බලය සමග සමතුලිතතාවට පත්වෙයි. එවිට වස්තුවට යෙදෙන මුළු බලය ශුන්ය නිසා එය චලනය නොවෙයි. වස්තුව
චලනය කිරීමට සෑහෙන තරම් බලයක් යෙදූ විට එය සමතුලිත කිරීමට ප්රතිරෝධී බලයට නොහැකි වේ. එම නිසා සමතුලිත නොවූ බලයක් (අසමතුලිත බලයක් – unbalanced force) ඉතිරි වී වස්තුව චලනය වීම ආරම්භ වෙයි. ඉහත සඳහන් මේසය අයිස් වැනි ඉතා සුමට පෘෂ්ඨයක් මත තබා තිබුණේ නම් ඉතා කුඩා බලයකින් වුව ද එහි චලිතය ආරම්භ කළ හැකි වෙයි. එසේ වන්නේ ප්රතිරෝධී බලය නොසැලකිය හැකි තරම් කුඩා වීම හේතුවෙන් අප යොදන මුළු බලයම අසමතුලිත බලයක් ලෙස මේසයේ චලිතයට දායක වීම නිසා ය. නිශ්චලතාවයේ පවතින වස්තුවක් මත අසමතුලිත බලයක් ක්රියාකරන ඕනෑම අවස්ථාවක එම වස්තුව චලනය වීම ආරම්භවෙයි.

4.3 රූපයේ පෙන්වා ඇත්තේ බර පැටවූ කරත්තයක් ගොනෙකු විසින් ඇදගෙන යන අවස්ථාවකි. කෙනෙක් කරත්තය
පසුපස සිට එය චලනය වන දිශාවට බලයක් යෙදුවහොත් සිදුවන්නේ කරත්තය චලනය වන ප්රවේගය වැඩි වීම ය. කරත්තය චලනය වන දිශාවට විරුද්ධ අතට බලයක් යෙදුවහොත් එහි ප්රවේගය අඩු වන්නේ ය. මෙයින් පෙනෙන්නේ බලයක් යෙදීමෙන් ලැබෙන ඵලය, එම බලයේ දිශාව අනුව වෙනස් වන බවය.
මෙයින් අපට පැහැදිලි වන කරුණක් වනුයේ බලයට විශාලත්වයක් මෙන් ම දිශාවක් ද ඇති බවයි. ඒ නිසා බලය දෛශික රාශියකි. යම් ලක්ෂ්යයක් මත බලයක් ක්රියා කරන දිශාව එම ලක්ෂ්යයේ සිට අඳින ලද සරල රේඛාවකින් දැක්විය හැකි අතර එයට බලයේ ක්රියා රේඛාව යැයි කියනු ලැබේ. බලය සහ චලිතය පිළිබඳ ව අපි අත්දකින දේ සර් අයිසැක් නිව්ටන් නැමැති සුප්රසිද්ධ විද්යාඥයා විසින් ගැඹුරු ලෙස අධ්යයනය කර නියම තුනක් ඉදිරිපත් කර ඇත. දැන් අපි ඒ එක් එක් නියමය පිළිබඳව විමසා බලමු.
■ නිව්ටන්ගේ පළමු වන නියමය
බාහිර අසමතුලිත බලයක් යෙදෙන තුරු නිශ්චල වස්තූන් නිශ්චලතාවයේම පවතින අතර, චලනය වන වස්තූන් ඒකාකාර ප්රවේගයෙන් චලනය වේ.
නිශ්චල ව පවතින වස්තූන් බාහිර බල රහිත ව චලිතය ආරම්භ නොකරන බව අපි එදිනෙදා ජීවිතයේ දී අත්දකින කරුණකි. නමුත්, අපි එදිනෙදා ජීවිතයේ දී බොහෝ විට දකින්නේ චලනය වන වස්තූන් දිගට ම චලනය නොවී බාහිර බලයකින් තොර ව නිශ්චලතාවට පත්වන බවකි. මෙය පැහැදිලි කර ගැනීමට පහත නිදසුන සලකා බලමු.
කැරම් ලෑල්ලක් මත තිබෙන කැරම් ඩිස්කයට (disk) 4.4 රූපයේ පෙන්වා ඇති ආකාරයට නිය තුඩින් පහරක් එල්ල කරන අවස්ථාවක් සලකන්න. එවිට එම ඩිස්කය ලෑල්ල මත ටික දුරක් ගමන් කර නිශ්චල වේ. කැරම් ලෑල්ලට පුයර දමා හොඳින් මැදීමෙන් පසුව කැරම් ඩිස්කයට නැවතත් නිය තුඩින් පළමු තරමේ ම පහරක් එල්ල කළහොත් එය පෙරට වඩා බෙහෙවින් වැඩි දුරක් ගමන් කර නිශ්චලතාවට පත් වෙය

පුයර දැමූ විට සිදු වන්නේ කැරම් ඩිස්කයේ චලිතයට ඇති ප්රතිරෝධී බලය අඩු වීමයි. වස්තුවක් පෘෂ්ඨයක් මත චලනය වන විට එම චලිතයට බාධා පමුණුවන්නේ ඝර්ෂණ බලය යි. යම් ක්රමයකින් ඝර්ෂණ බලය ශුන්ය කළ හැකි නම් කැරම් ඩිස්කය නොනැවතී ගමන් කරනු ඇත.
මෙම නියමය හා සම්බන්ධ සාමාන්ය ජීවිතයේ අප අත්දකින තවත් අවස්ථාවක් සලකා බලමු. ගමන් කරන බස් රථයක් තුළ, මගියෙක් කිසිම ආධාරකයක් අල්ලා නොගෙන සිටගෙන සිටින්නේ යැයි සිතන්න. හදිසියේ බස් රථයට තිරිංග යොදා නවත්වනු ලැබුවහොත්, ඔහු ඉදිරි අතට වැටෙයි. මීට හේතුව කුමක් ද?
ඔහුගේ පාද බසයේ ස්පර්ශ ව තිබුණු නිසා බසය මගින් පාද මත බලයක් යොදා පාද නිශ්චලතාවට පත්කරයි. නමුත් ශරීරයේ උඩු කොටස මත එවැනි බලයක් නොයෙදෙන නිසා එම කොටසේ ප්රවේගයක් පවතී. ඔහු ඉදිරියට වැටෙන්නේ එබැවිනි.
දැන්, ඉහත කී මගියා සිටින්නේ නිශ්චලතාවයේ පවතින බස් රථයක් තුළ යැයි සිතන්න, ඔහු නොදැනුවත් ව බසය පණ ගන්වා චලිතය ඇරඹුව හොත් මෙම මගියා වැටෙන්නේ පසු අතට ය. බස් රථයේ චලිතය ආරම්භ වීමත් සමග රථයේ ස්පර්ශ ව තිබුණු පාදවලට බසය මගින් බලයක් යෙදීම නිසා ශරීරයේ පහළ ප්රදේශයට ප්රවේගයක් ලැබුණ ද ශරීරයේ උඩු කොටස තවමත් නිශ්චලතාවයේ ම පැවතීම නිසා මෙසේ සිදුවෙයි.
මෝටර් රථ තුළ ගමන් කරන විට ආසන පටි පැලදීම අවශ්ය වන්නේ, තිරිංග යෙදූ විට ඉදිරිපසට විසිවීමෙන් වැළකීමට ය. ආසන පටිය මගින් මගියාගේ ශරීරයේ ඉහළ කොටසටත් බලයක් යෙදෙන නිසා තිරිංග යෙදූ විට ද මුළු ශරීරය ම වාහනයේ ප්රවේගයේම පවතියි.

■ නිව්ටන්ගේ දෙවන නියමය
වස්තුවක ඇති වන ත්වරණය, එයට යොදනු ලබන අසමතුලිත බලයට අනුලෝම ව සමානුපාතික වන අතර, වස්තුවේ ස්කන්ධයට ප්රතිලෝම ව සමානුපාතික වේ.
මෙහි දී ත්වරණය, අසමතුලිත බලයට අනුලෝම ව සමානුපාතිකය යන්නෙන් අදහස් කරන්නේ එම බලයෙහි විශාලත්වය යම් අනුපාතයකින් අඩු හෝ වැඩි කළ විට එම අනුපාතයෙන් ම ත්වරණය ද අඩු හෝ වැඩි වන බවයි. සංකේතාත්මක ව එය a ∝ F ත් ලෙස ලියනු ලැබේ.
ත්වරණය, ස්කන්ධයට ප්රතිලෝම ව සමානුපාතිකය යන්නෙන් අදහස් කරන්නේ ස්කන්ධය යම් අනුපාතයකින් වැඩි කළහොත් ත්වරණය එම අනුපාතයෙන් අඩු වන බවත්, ස්කන්ධය යම් අනුපාතයකින් අඩු කළහොත් ත්වරණය එම අනුපාතයෙන් වැඩිවන බවත් ය. මෙම ප්රකාශය a ∝ 1/m ලෙස සංකේතාත්මක ව ලියනු ලැබේ.
එනම්, නිව්ටන්ගේ දෙවන නියමය අනුව,

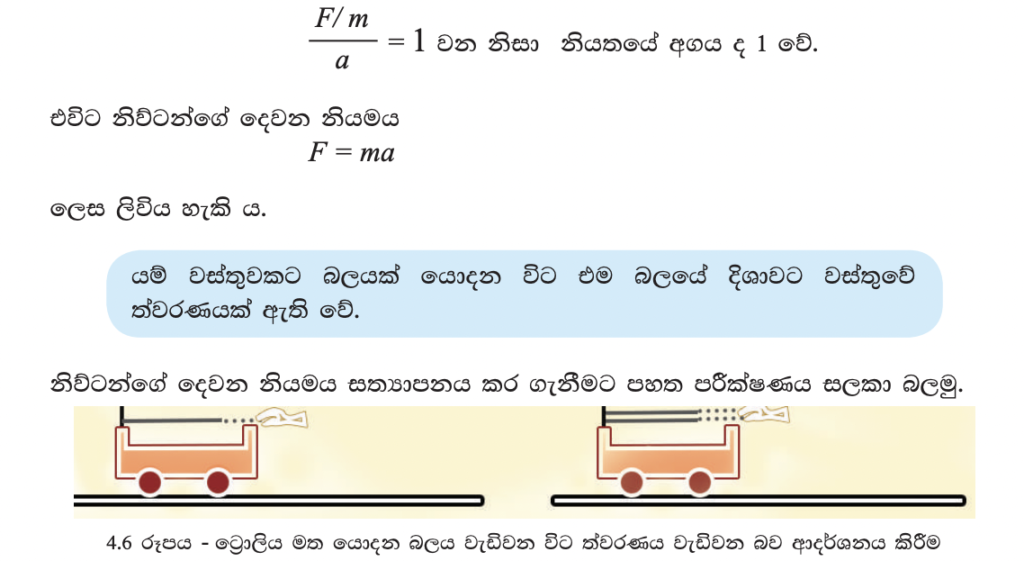
● තිරස් මේසයක් මත ට්රොලියක් තබා එයට රබර් පටියක් සම්බන්ධ කර ට්රොලිය එක අතකින් අල්ලා ගන්න.
● අනෙක් අතින් රබර් පටියේ නිදහස් කෙළවර අල්ලා ගෙන එය 4.6 රූපයේ පෙන්වා ඇති ආකාරයට ට්රොලියේ අනෙක් කෙළවර දක්වා ඇදෙන පරිදි අදින්න.
● ඉන් පසු ට්රොලිය නිදහස් කර රබර් පටියේ ඇදුණු කොටස නොවෙනස් ව පවතින අයුරින්, ට්රොලිය සමග අත චලනය කරන්න. එවිට ට්රොලිය ත්වරණයෙන් චලනය වන
බව ඔබට නිරීක්ෂණය කළ හැකි වනු ඇත.
● ට්රොලියට පළමු රබර් පටියට සමාන තවත් රබර් පටියක් සම්බන්ධ කර, රබර් පටි දෙක ම පළමු ප්රමාණයට ඇද, පෙර පරිදි ම පරීක්ෂණය කර ට්රොලියේ චලිතය
නිරීක්ෂණය කරන්න. මෙම අවස්ථාවේ ට්රොලිය මත යෙදෙන බලය පළමු අවස්ථාවේ මෙන් දෙගුණයකි. ට්රොලියේ ත්වරණය මුල් අවස්ථාවට වඩා වැඩි වන බව
නිරීක්ෂණය කළ හැකි වනු ඇත.
● ඉන් පසු එක සමාන රබර් පටි තුනක් සම්බන්ධ කර ඉහත පරීක්ෂණය ම කර ට්රොලියේ චලිතය නිරීක්ෂණය කරන විට ට්රොලියේ ත්වරණය දෙවන අවස්ථාවට වඩා වැඩි
වන බව නිරීක්ෂණය කළ හැකි ය. එක සමාන රබර් පටි තුනක් යොදන නිසා මෙහි දී ට්රොලිය මත යෙදෙන බලය පළමු අවස්ථාවේ මෙන් තුන් ගුණයකි.
● මේ අනුව ට්රොලියට යොදන බලය වැඩි වන විට ට්රොලිය චලිතය වන ත්වරණය ද වැඩි වන බව නිරීක්ෂණය කළ හැකි ය.
● ඉන්පසු ට්රොලිය මත යම් ස්කන්ධයක් තබා එක් රබර් පටියක් යොදා පරීක්ෂණය නැවත ස ිදු කර එහි චලිතය නිරීක්ෂණය කරන්න. එවිට ත්වරණය අඩු වන බව
නිරීක්ෂණය කළ හැකි වනු ඇත.
● ඉන් පසු තවත් ස්කන්ධයක් ට්රොලිය මත තබා පෙර පරිදි ම පරීක්ෂණය කළ විට ත්වරණය තවත් අඩු වන බව නිරීක්ෂණය කළ හැකි ය.
මින් පැහැදිලි වන්නේ, යොදන බලය නියතව පවතින්නේ නම් ස්කන්ධය වැඩි වන තරමට ත්වරණය අඩු වන බවයි.
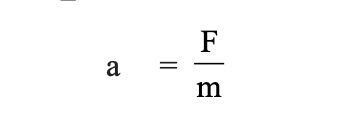
■ නිව්ටන්ගේ තුන්වන නියමය
මෙහි දී ක්රියාවක් (action) යනුවෙන් අදහස් කෙරෙන්නේ යම් වස්තුවක් මගින් තවත් වස්තුවක් මත යෙදෙන බලයකි. එවිට ප්රතික්රියාව (reaction) වන්නේ දෙවන වස්තුව මගින් පළමු වස්තුව මත යෙදෙන බලයකි. රබර් බැලූනයකින් වාතය පිට වීම මෙම නියමය යෙදෙන එක් ප්රායෝගික අවස්ථාවකි. වාතය පිරවූ බැලූනයක, කට පහළට හරවා ගෙන අතින් අල්ලා ගෙන සිටින්න. 4.7 රූපයේ පරිදි බැලූනයේ කට බුරුල් කර අත හරින්න. බැලූනය වේගයෙන් ඉහළ ගොස් පසුව බිමට වැටෙනු දැකිය හැකි ය. බැලූනයෙන් වාතය පිටවන්නේ එහි රබර් බිත්ති මගින් වාත අනු පහළට තල්ලු කරන නිසා ය. බැලූනය ඉහළ යන්නේ පිටවන වාත අනු මගින් බැලූනය මත යොදන ප්රතික්රියා බලයෙන
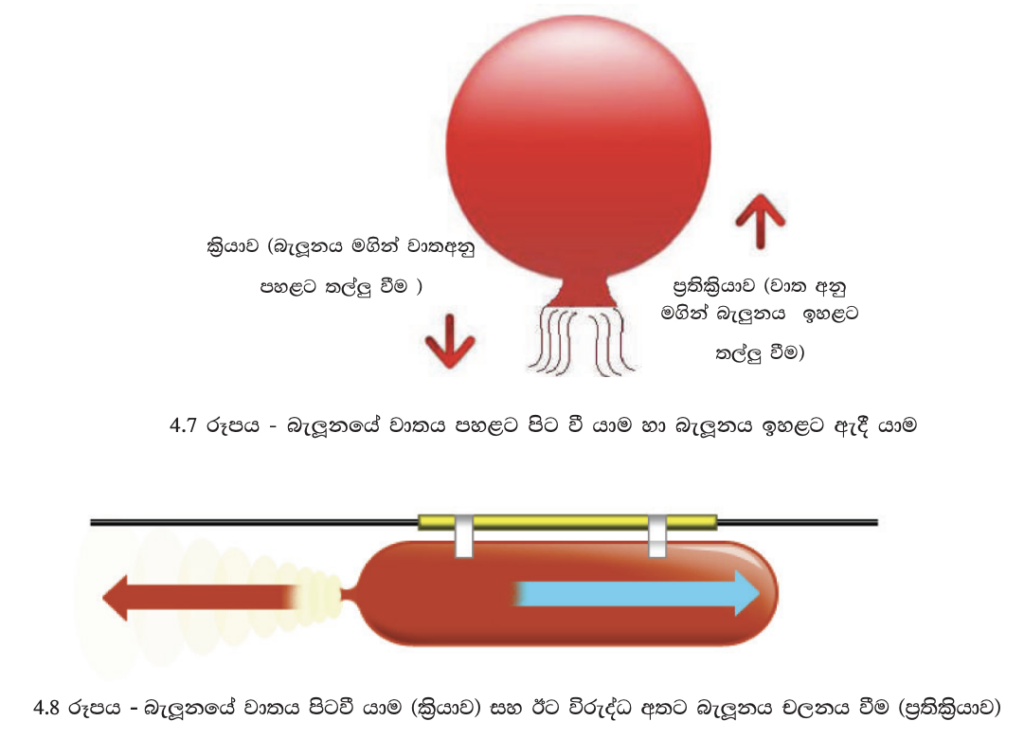
බැලූනයකින් වාතය පිට වීම නිසා බැලූනය ගමන් කිරීම 4.8 රූපයේ දැක්වෙන ආකාරයට ද දැකගත හැකි ය. රූපයේ දැක්වෙන පරිදි වාතය පිරවූ බැලූනයක් සෙලෝටේප් කැබලි ආධාරයෙන් බීම බට කැබැල්ලකට සම්බන්ධ කරගන්න. ඉන් පසු බීම බටය තුළින් කම්බියක් රිංගවා එම කම්බිය තිරස් ව සිටින සේ දෙපසින් රඳවන්න. දැන් බැලූනයේ කටෙහි ගැටගසා ඇති නූල බුරුල් කර බැලූනයෙන් වාතය ඉවතට යාමට ඉඩ දෙන්න. වාතය පිට වී යන දිශාවට විරුද්ධ අතට බැලූනය කම්බිය දිගේ ගමන් කරනු දැකිය හැකි ය.
ක්රියාව සහ ප්රතික්රියාව දැක ගත හැකි තවත් අවස්ථාවක් 4.9 රූපයේ පෙන්වා ඇත. වීදුරු බෝල කිහිපයක් මත ලෑලි කැබලි දෙකක් තබන්න. මෙම ලෑලි දෙක මත දෙදෙනකු වාඩි කරවන්න. ඉන් පසු රූපයේ දැක්වෙන පරිදි අත්ලට අත්ල තබා එකිනෙකා තල්ලු කර ගතහොත් දෙදෙනා ම ප්රතිවිරුද්ධ දිශාවට තල්ලු වී යනු ඇත.

නිව්ටන්ගේ තුන්වන නියමය යෙදෙන තවත් ප්රායෝගික අවස්ථා කිහිපයක් පහතින් දක්වා ඇත.
ඔරුවක් පදින විට (4.10 රූපය) කෙරෙන්නේ හබලෙන් ජලය පසු පසට තල්ලු කිරීම යි. එනම් බලය යොදන්නේ හබලෙන් ජලය වෙතයි. එවිට ජලය මගින් හබල මත යෙදෙන ප්රතික්රියාව නිසා ඔරුව ඉදිරියට ගමන් කරය

පිහිනීමේ දී (4.11 රූපය) දෑතින් ජලය මත බලය යොදන්නේ පසුපසට ය. එවිට ජලයෙන් ශරීරය මත බලය යෙදෙන්නේ ඉදිරි අතට යි. ඒ නිසා ඉදිරියට තල්ලු වී යයි. මෙහි දී දෑතින් පිටුපසට යොදන බලය ක්රියාවයි. එම ක්රියාවේ ප්රතික්රියාව ශරීරය මත ඉදිරියට ඇතිවන බලය යි.


Responses