දුර හා විස්ථාපනය
දුර (distence) යනු ඔබට හුරු පුරුදු සංකල්පයකි. ඔබ නිවසේ සිට පාසලට යන විට යම් දුරක් ගෙවා යා යුතු ය. සමහර විට නිවසේ සිට පාසලට යා හැකි මාර්ග කිහිපයක් තිබිය හැකි ය. ඉන් සමහරක් දුර වැඩි මාර්ග වන අතර සමහරක් දුර අඩු ඒවා විය හැකි ය. ළමයකුට A නම් ස්ථානයේ සිට B නම් වෙනත් ස්ථානයක් දක්වා ගමන් කළ හැකි මාර්ග කිහිපයක් 2.1 රූපයේ දැක්වේ.

A සිට P මාර්ගයේ ගමන් කළහොත් A හා B අතර දුර 320 ප වේ. Q මාර්ගයේ ගමන් කළහොත් දුර 200 ප වේ. ඍ මාර්ගය තෝරාගත හොත් දුර 240 ප වේ. මෙයින් පෙනෙන්නේ දුර ආරම්භක සහ අවසාන ස්ථාන මත පමණක් නොව ගමන් කරන මාර්ගය අනුව ද වෙනස් වන බව ය.
A ස්ථානයෙන් පටන් ගෙන B ස්ථානයට ළගා වීම සඳහා ළමයා මේ කවර මාර්ගය තෝරාගත්ත ද එහි අවසාන ප්රතිඵලය වන්නේ ළමයා සිටින ස්ථානය A සිට සරල රේඛීයව 160 ප දුරක් නැගෙනහිර දිශාවට පිහිටි B දක්වා වෙනස් වීමයි. මේ ආකාරයට එක් ස්ථානයක සිට තවත් ස්ථානයක් කරා යම් දිශාවකට සිදු වන සරල රේඛීය ඈත් වීම විස්ථාපනය (displacement) නම් වේ. විස්ථාපනයේ විශාලත්වය වන්නේ ස්ථාන දෙක අතර සරල රේඛීය දුරය
කිසියම් භෞතික රාශියක අගය ප්රකාශ කිරීමේ දී විශාලත්වයක් පමණක් ප්රකාශ කිරීම සෑහේ නම් එය අදිශ රාශියක් ලෙස හැඳින්වේ.
උදා : දුර, වේගය, ස්කන්ධය, කාලය
කිසියම් භෞතික රාශියක අගය ප්රකාශ කිරීමේ දී විශාලත්වයට අමතරව දිශාවක් අවශ්ය වේ නම් එය දෛශික රාශියක් ලෙස හැඳින්වේ.
උදා : විස්ථාපනය, ප්රවේගය, ත්වරණය, බර
ඉහත සඳහන් උදාහරණයෙහි ළමයාගේ විස්ථාපනය නැගෙනහිරට 160 m වේ. ගමන් ගන්නා මාර්ගය අනුව දුර වෙනස් වුව ද, විස්ථාපනය එකම අගයක් ගෙන ඇත. මීට අමතර ව දුර සහ විස්ථාපනය අතර තවත් වැදගත් වෙනසක් ඇත. දුර මැනීමේ දී අප ගමන් කළ දිශාව නොසලකන නිසා දුරට විශාලත්වයක් තිබුණ ද දිශාවක් නොමැත. එබැවින් දුර අදිශ රාශියකි. නමුත් විස්ථාපනය මැනීමේ දී කුමන දිශාවකට විස්ථාපනය සිදුවූයේ ද යන්න වැදගත් ය. එනම් විස්ථාපනයට විශාලත්වයක් මෙන්ම දිශාවක් ද ඇත. ඒ නිසා විස්ථාපනය දෛශික රාශියකි.
■ දුර සහ විස්ථාපනය පිළිබඳ ව පහත උදාහරණ මගින් තවදුරටත් විමසා බලමු.

මෙම මාර්ගය දිගේ ළමයා ගමන් කළ දුර 400 ප වුව ද, ළමයාගේ විස්ථාපනයේ විශාලත්වය 120 m වන අතර දිශාව AB වේ.
(iii) ධාවන තරග සඳහා යොදා ගන්නා 200 ප ධාවන පථයක් 2.4 රූපයේ දැක්වේ.
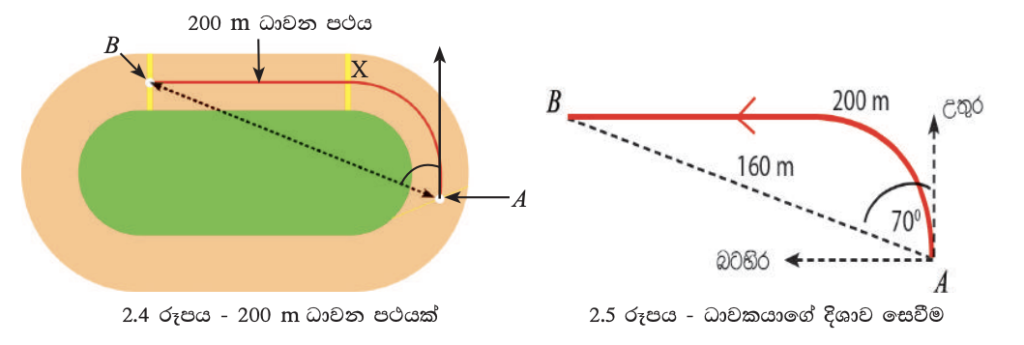
විශාලත්වය 160 m වේ. 2.5 රූපය අනුව ඔහුගේ විස්ථාපනයේ දිශාව උතුරෙන් 700 ක් බටහිරට යි. එම විස්ථාපනය පහත දැක්වෙන ආකාරයට ලිවිය හැකි ය.

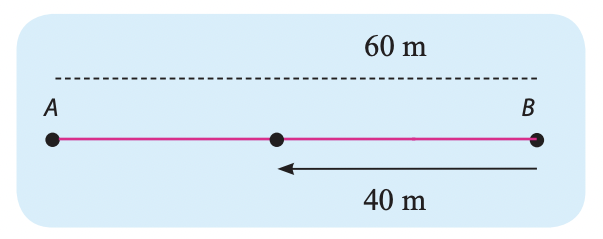
(iv) දැන් 2.6 රූපයේ දැක්වෙන පරිදි සරල රේඛීය මාර්ගයක් දිගේ ළමයෙක් A හි සිට B දක්වා 60m දුරක් ගමන් කරන අවස්ථාවක් සලකන්න.

ළමයාගේ විස්ථාපනය AB දිශාවට 60m වෙයි. ඉන්පසු ළමයා එම දිශාවට ම තවත A 40m දුරක් ගමන් කර ක් වෙත පැමිණියහොත් සම්පූර්ණ විස්ථාපනය කොපමණ වේ ද? විස්ථාපන දෙකක් හෝ වැඩි ගණනක් එක ම දිශාවට සිදු වී ඇති විට ඒවා අංක ගණිතය භාවිතයෙන් එකතු කිරීමට හෝ අඩු කිරීමට ඔබට හැකි ය.
මෙහි දී විස්ථාපන දෙකම එකම දිශාවට පිහිටන බැවින්,
සම්පූර්ණ විස්ථාපනය = 60 m + 40 m = 100 m
එනම් දැන් ළමයා සිටින්නේ ආරම්භක ස්ථානයෙන් සරල රේඛීය ව 100 ප ඈතිනි.
දැන්, 2.7 රූපයේ පෙන්වා ඇති ආකාරයට ළමයා A සිට B දක්වා ගමන් කර ඊ සිට ඉදිරියට නොගොස් ආපසු 40m ගමන් කළේ යැයි සිතන්න. එවිට 40m ට අදාළ විස්ථාපනයේ දිශාව A සිට B ට අදාළ විස්ථාපනයේ දිශාවට ප්රතිවිරුද්ධ දිශාවට බව පෙනේ. එමනිසා, මෙහි දී ද ගමන් කළ දුර 100m වුව ද සම්පූර්ණ විස්ථාපනය වනුයේ 60m + (- 40 m) ය. එනම් දැන් විස්ථාපනය වනුයේ 20m ප්රමාණයකි.
ළමයා A සිට B දක්වා ගමන් කළ දුර ම යළි විරුද්ධ දෙසට ගමන් කළේ නම්, විස්ථාපනය 60 m + (- 60 m) වේ. එනම් විස්ථාපනය ශුන්ය (0) වේ. ඉන් අප දැන ගන්නේ ළමයා චලිතය ඇරඹි ස්ථානයේ ම දැන් සිටින බවයි.
